ما هو تصنيف سولو؟
ظهر تصنيف سولو في أواخر السبعينيات على يد العالِمين بيغز (Biggs) وكوليس (Collis)، وهو اختصار لعبارة: Structure of the Observed Learning Outcome
أي: بنية ناتج التعلّم المُلاحظ.
يقوم التصنيف على فكرة بسيطة لكنها عميقة: “كلما ازدادت قدرة المتعلم على ربط الأفكار وتحليلها وتطبيقها في مواقف جديدة، ارتفع مستوى فهمه”.
مستويات تصنيف سولو الخمسة:
يتكوّن التصنيف من خمسة مستويات متدرجة تعبّر عن تطور الفهم من البسيط إلى المعقد، وهي:
1. ما قبل البنائي (Prestructural)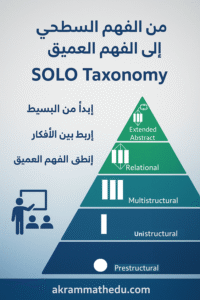 المتعلم لا يمتلك فهمًا ذا معنى بعد، وقد يقدّم استجابات عشوائية أو غير مترابطة.
المتعلم لا يمتلك فهمًا ذا معنى بعد، وقد يقدّم استجابات عشوائية أو غير مترابطة.
2. أحادي البنية (Unistructural)
يركّز المتعلم على جانب واحد فقط من المفهوم دون إدراك للعلاقات.
3. متعدد البنية (Multistructural) يتعامل المتعلم مع عدة عناصر، لكنه ما زال ينظر إليها كأجزاء منفصلة.
4. علاقي (Relational)
يبدأ المتعلم بربط الأفكار ببعضها، ويرى المفهوم ككلٍّ مترابط.
5. مجرد ممتد (Extended Abstract)
أرقى مستويات الفهم؛ حيث يستخدم المتعلم المفهوم في مواقف جديدة ويولّد أفكارًا أو حلولًا مبتكرة.
تطبيقات تصنيف سولو في تعليم الرياضيات
يساعد تصنيف سولو المعلم في تخطيط الدروس، وتصميم الأنشطة، وبناء أدوات التقويم وفق مستويات التفكير المطلوبة.
فعلى سبيل المثال، يمكن للمعلم عند تدريس موضوع في الجبر أو الهندسة أن ينتقل تدريجيًا مع طلابه من:
- تعريف المفهوم (مستوى أحادي البنية)،
تُعد خرائط التفكير العميق (HOT SOLO Maps) أدوات بصرية تساعد المتعلمين على التعبير عن مستوى فهمهم من خلال الرسم أو التنظيم المفهومي للأفكار.
- إلى تطبيقات متعددة (متعدد البنية)،
- ثم تحليل العلاقات بين المتغيرات (علاقي)،
- وأخيرًا توظيفها في مواقف جديدة أو ابتكار أنماط جديدة من الحل (مجرد ممتد).
خرائط التفكير العميق وفق نموذج سولو (HOT SOLO Maps)
تتيح هذه الخرائط للطالب أن يرى بنفسه تطور فهمه، وللمعلم أن يقيس بدقة مستوى التفكير الذي وصل إليه المتعلم.
سداسيات سولو (SOLO Hexagons)
أداة تعليمية تفاعلية تتكون من سداسيات تحمل مفاهيم أو أفكارًا، ويُطلب من الطلاب ربطها بطريقة منطقية لتمثيل فهمهم العميق للعلاقات.
تُستخدم هذه الأداة بفاعلية في دروس الرياضيات لتوضيح العلاقات بين المفاهيم، مثل:
الزوايا، المتطابقات المثلثية، أو العلاقات الجبرية، في سياق تعلّم قائم على التحليل والتركيب.
نحو تعليم قائم على الفهم العميق
إن اعتماد تصنيف سولو في تعليم الرياضيات يفتح آفاقًا جديدة أمام المعلمين والطلاب على حد سواء، إذ يتحوّل الدرس من نقل معلومات إلى بناء تفكير، ومن حل مسائل إلى حل مشكلات وفهم نماذج.
فالمتعلم الذي يسير وفق مستويات سولو يتعلم كيف يفكر لا ماذا يفكر، ويصبح أكثر قدرة على توظيف معرفته في مواقف الحياة الواقعية.
يبقى تصنيف سولو إطارًا ثريًا لكل معلم يسعى إلى تطوير ممارساته التدريسية نحو تعليم قائم على الفهم العميق.
وفي كتبي وأبحاثي حول هذا المجال، أقدّم نماذج عملية وخرائط تفكير يمكن أن تسهم في جعل الرياضيات مادة للتفكير والإبداع، لا للحفظ والتقليد.